与程序员相关的CPU缓存知识

2020年03月01日陈皓评论 111 条评论 173,523 人阅读

好久没有写一些微观方面的文章了，今天写一篇关于CPU Cache相关的文章，这篇文章比较长，主要分成这么几个部分：基础知识、缓存的命中、缓存的一致性、相关的代码示例和延伸阅读。其中会讲述一些多核 CPU 的系统架构以及其原理，包括对程序性能上的影响，以及在进行并发编程的时候需要注意到的一些问题。这篇文章我会尽量地写简单和通俗易懂一些，主要是讲清楚相关的原理和问题，而对于一些细节和延伸阅读我会在文章最后会给出相关的资源。

因为无论你写什么样的代码都会交给CPU来执行，所以，如果你想写出性能比较高的代码，这篇文章中提到的技术还是值得认真学习的。另外，千万别觉得这些东西没用，这些东西非常有用，十多年前就是这些知识在性能调优上帮了我的很多大忙，从而跟很多人拉开了差距……

基础知识

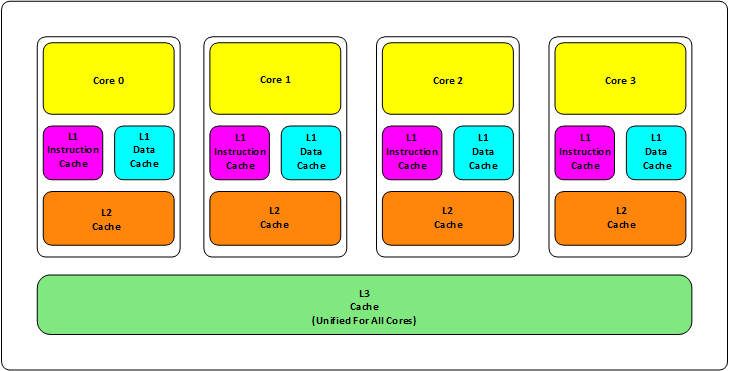
首先，我们都知道现在的CPU多核技术，都会有几级缓存，老的CPU会有两级内存（L1和L2），新的CPU会有三级内存（L1，L2，L3 ），如下图所示：

其中：

L1缓存分成两种，一种是指令缓存，一种是数据缓存。L2缓存和L3缓存不分指令和数据。
L1和L2缓存在每一个CPU核中，L3则是所有CPU核心共享的内存。
L1、L2、L3的越离CPU近就越小，速度也越快，越离CPU远，速度也越慢。

再往后面就是内存，内存的后面就是硬盘。我们来看一些他们的速度：

L1 的存取速度：4 个CPU时钟周期
L2 的存取速度： 11 个CPU时钟周期
L3 的存取速度：39 个CPU时钟周期
RAM内存的存取速度：107 个CPU时钟周期

我们可以看到，L1的速度是RAM的27倍，但是L1/L2的大小基本上也就是KB级别的，L3会是MB级别的。例如：Intel Core i7-8700K ，是一个6核的CPU，每核上的L1是64KB（数据和指令各32KB），L2 是 256K，L3有2MB（我的苹果电脑是 Intel Core i9-8950HK，和Core i7-8700K的Cache大小一样）。

我们的数据就从内存向上，先到L3，再到L2，再到L1，最后到寄存器进行CPU计算。为什么会设计成三层？这里有下面几个方面的考虑：

一个方面是物理速度，如果要更大的容量就需要更多的晶体管，除了芯片的体积会变大，更重要的是大量的晶体管会导致速度下降，因为访问速度和要访问的晶体管所在的位置成反比，也就是当信号路径变长时，通信速度会变慢。这部分是物理问题。
另外一个问题是，多核技术中，数据的状态需要在多个CPU中进行同步，并且，我们可以看到，cache和RAM的速度差距太大，所以，多级不同尺寸的缓存有利于提高整体的性能。

这个世界永远是平衡的，一面变得有多光鲜，另一面也会变得有多黑暗。建立这么多级的缓存，一定就会引入其它的问题，这里有两个比较重要的问题，

一个是比较简单的缓存的命中率的问题。
另一个是比较复杂的缓存更新的一致性问题。

尤其是第二个问题，在多核技术下，这就很像分布式的系统了，要对多个地方进行更新。

缓存的命中

在说明这两个问题之前。我们需要要解一个术语 Cache Line。缓存基本上来说就是把后面的数据加载到离自己近的地方，对于CPU来说，它是不会一个字节一个字节的加载的，因为这非常没有效率，一般来说都是要一块一块的加载的，对于这样的一块一块的数据单位，术语叫“Cache Line”，一般来说，一个主流的CPU的Cache Line 是 64 Bytes（也有的CPU用32Bytes和128Bytes），64Bytes也就是16个32位的整型，这就是CPU从内存中捞数据上来的最小数据单位。

比如：Cache Line是最小单位（64Bytes），所以先把Cache分布多个Cache Line，比如：L1有32KB，那么，32KB/64B = 512 个 Cache Line。

一方面，缓存需要把内存里的数据放到放进来，英文叫 CPU Associativity。Cache的数据放置的策略决定了内存中的数据块会拷贝到CPU Cache中的哪个位置上，因为Cache的大小远远小于内存，所以，需要有一种地址关联的算法，能够让内存中的数据可以被映射到Cache中来。这个有点像内存地址从逻辑地址向物理地址映射的方法，但不完全一样。

基本上来说，我们会有如下的一些方法。

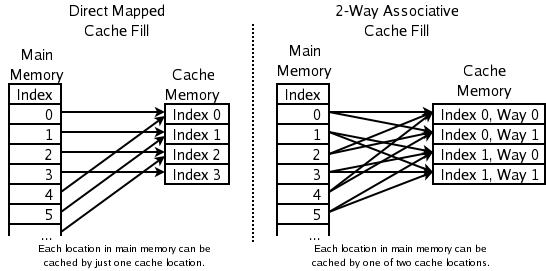
一种方法是，任何一个内存地址的数据可以被缓存在任何一个Cache Line里，这种方法是最灵活的，但是，如果我们要知道一个内存是否存在于Cache中，我们就需要进行O(n)复杂度的Cache遍历，这是很没有效率的。
另一种方法，为了降低缓存搜索算法，我们需要使用像Hash Table这样的数据结构，最简单的hash table就是做“求模运算”，比如：我们的L1 Cache有512个Cache Line，那么，公式：（内存地址 mod 512）* 64 就可以直接找到所在的Cache地址的偏移了。但是，这样的方式需要我们的程序对内存地址的访问要非常地平均，不然冲突就会非常严重。这成了一种非常理想的情况了。
为了避免上述的两种方案的问题，于是就要容忍一定的hash冲突，也就出现了 N-Way 关联。也就是把连续的N个Cache Line绑成一组，然后，先把找到相关的组，然后再在这个组内找到相关的Cache Line。这叫 Set Associativity。如下图所示。

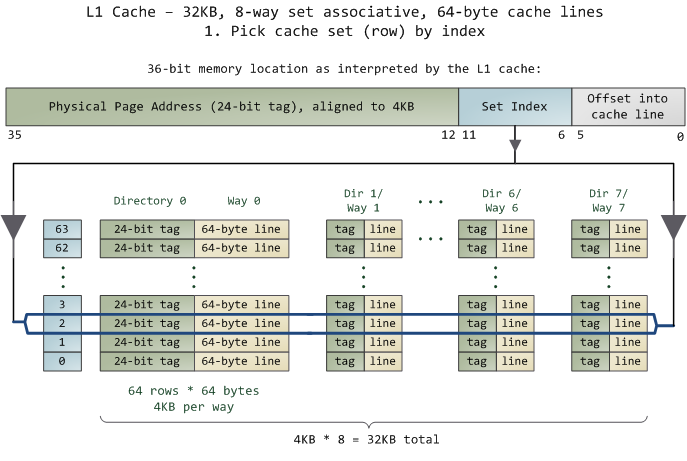
对于 N-Way 组关联，可能有点不好理解，这里个例子，并多说一些细节（不然后面的代码你会不能理解），Intel 大多数处理器的L1 Cache都是32KB，8-Way 组相联，Cache Line 是64 Bytes。这意味着，

32KB的可以分成，32KB / 64 = 512 条 Cache Line。
因为有8 Way，于是会每一Way 有 512 / 8 = 64 条 Cache Line。
于是每一路就有 64 x 64 = 4096 Byts 的内存。

为了方便索引内存地址，

Tag：每条 Cache Line 前都会有一个独立分配的 24 bits来存的 tag，其就是内存地址的前24bits
Index：内存地址后续的6个bits则是在这一Way的是Cache Line 索引，2^6 = 64 刚好可以索引64条Cache Line
Offset：再往后的6bits用于表示在Cache Line 里的偏移量

如下图所示：（图片来自《Cache: a place for concealment and safekeeping》）

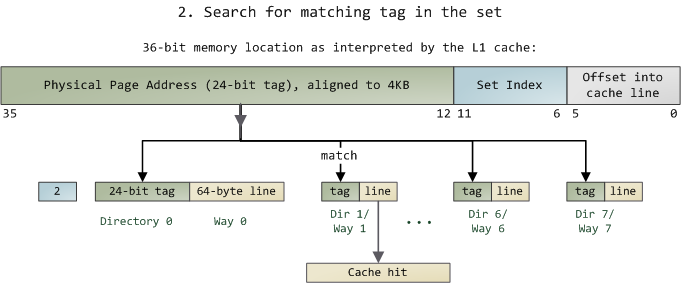
当拿到一个内存地址的时候，先拿出中间的 6bits 来，找到是哪组。

然后，在这一个8组的cache line中，再进行O(n) n=8 的遍历，主是要匹配前24bits的tag。如果匹配中了，就算命中，如果没有匹配到，那就是cache miss，如果是读操作，就需要进向后面的缓存进行访问了。L2/L3同样是这样的算法。而淘汰算法有两种，一种是随机一种是LRU。现在一般都是以LRU的算法（通过增加一个访问计数器来实现）

这也意味着：

L1 Cache 可映射 36bits 的内存地址，一共 2^36 = 64GB的内存
当CPU要访问一个内存的时候，通过这个内存中间的6bits 定位是哪个set，通过前 24bits 定位相应的Cache Line。
就像一个hash Table的数据结构一样，先是O(1)的索引，然后进入冲突搜索。
因为中间的 6bits 决定了一个同一个set，所以，对于一段连续的内存来说，每隔4096的内存会被放在同一个组内，导致缓存冲突。

此外，当有数据没有命中缓存的时候，CPU就会以最小为Cache Line的单元向内存更新数据。当然，CPU并不一定只是更新64Bytes，因为访问主存实在是太慢了，所以，一般都会多更新一些。好的CPU会有一些预测的技术，如果找到一种pattern的话，就会预先加载更多的内存，包括指令也可以预加载。这叫 Prefetching 技术（参看，Wikipedia 的 Cache Prefetching 和纽约州立大学的 Memory Prefetching）。比如，你在for-loop访问一个连续的数组，你的步长是一个固定的数，内存就可以做到prefetching。（注：指令也是以预加载的方式执行，参看本站的《代码执行的效率》中的第三个示例）

了解这些细节，会有利于我们知道在什么情况下有可以导致缓存的失效。

缓存的一致性

对于主流的CPU来说，缓存的写操作基本上是两种策略（参看本站《缓存更新的套路》），

一种是Write Back，写操作只要在cache上，然后再flush到内存上。
一种是Write Through，写操作同时写到cache和内存上。

为了提高写的性能，一般来说，主流的CPU（如：Intel Core i7/i9）采用的是Write Back的策略，因为直接写内存实在是太慢了。

好了，现在问题来了，如果有一个数据 x 在 CPU 第0核的缓存上被更新了，那么其它CPU核上对于这个数据 x 的值也要被更新，这就是缓存一致性的问题。（当然，对于我们上层的程序我们不用关心CPU多个核的缓存是怎么同步的，这对上层的代码来说都是透明的）

一般来说，在CPU硬件上，会有两种方法来解决这个问题。

Directory 协议。这种方法的典型实现是要设计一个集中式控制器，它是主存储器控制器的一部分。其中有一个目录存储在主存储器中，其中包含有关各种本地缓存内容的全局状态信息。当单个CPU Cache 发出读写请求时，这个集中式控制器会检查并发出必要的命令，以在主存和CPU Cache之间或在CPU Cache自身之间进行数据同步和传输。
Snoopy 协议。这种协议更像是一种数据通知的总线型的技术。CPU Cache通过这个协议可以识别其它Cache上的数据状态。如果有数据共享的话，可以通过广播机制将共享数据的状态通知给其它CPU Cache。这个协议要求每个CPU Cache 都可以“窥探”数据事件的通知并做出相应的反应。如下图所示，有一个Snoopy Bus的总线。

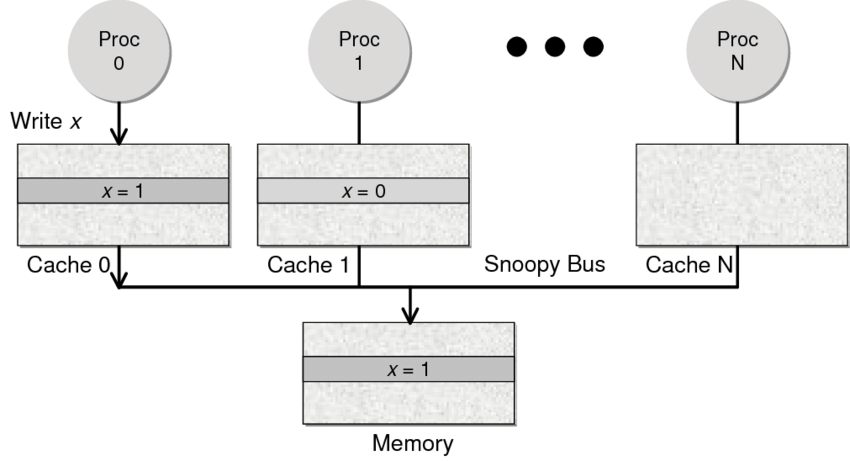
因为Directory协议是一个中心式的，会有性能瓶颈，而且会增加整体设计的复杂度。而Snoopy协议更像是微服务+消息通讯，所以，现在基本都是使用Snoopy的总线的设计。

这里，我想多写一些细节，因为这种微观的东西，让人不自然地就会跟分布式系统关联起来，在分布式系统中我们一般用Paxos/Raft这样的分布式一致性的算法。而在CPU的微观世界里，则不必使用这样的算法，原因是因为CPU的多个核的硬件不必考虑网络会断会延迟的问题。所以，CPU的多核心缓存间的同步的核心就是要管理好数据的状态就好了。

这里介绍几个状态协议，先从最简单的开始，MESI协议，这个协议跟那个著名的足球运动员梅西没什么关系，其主要表示缓存数据有四个状态：Modified（已修改）, Exclusive（独占的）,Shared（共享的），Invalid（无效的）。

这些状态的状态机如下所示（有点复杂，你可以先不看，这个图就是想告诉你状态控制有多复杂）：

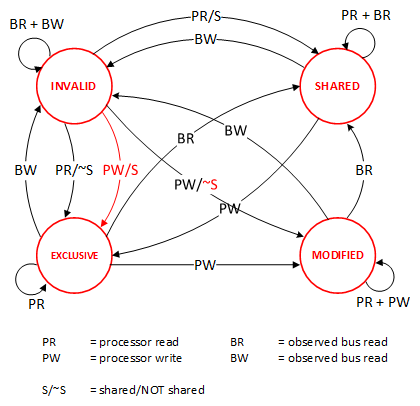
下面是个示例（如果你想看一下动画演示的话，这里有一个网页（MESI Interactive Animations），你可以进行交互操作，这个动画演示中使用的Write Through算法）：

当前操作	CPU0	CPU1	Memory	说明
1) CPU0 read(x)	x=1 (E)		x=1	只有一个CPU有 x 变量，所以，状态是 Exclusive
2) CPU1 read(x)	x=1 (S)	x=1(S)	x=1	有两个CPU都读取 x 变量，所以状态变成 Shared
3) CPU0 write(x,9)	x=9 (M)	x=1(I)	x=1	变量改变，在CPU0中状态变成 Modified，在CPU1中状态变成 Invalid
4) 变量 x 写回内存	x=9 (M)	X=1(I)	x=9	目前的状态不变
5) CPU1 read(x)	x=9 (S)	x=9(S)	x=9	变量同步到所有的Cache中，状态回到Shared

MESI 这种协议在数据更新后，会标记其它共享的CPU缓存的数据拷贝为Invalid状态，然后当其它CPU再次read的时候，就会出现 cache miss 的问题，此时再从内存中更新数据。从内存中更新数据意味着20倍速度的降低。我们能不能直接从我隔壁的CPU缓存中更新？是的，这就可以增加很多速度了，但是状态控制也就变麻烦了。还需要多来一个状态：Owner(宿主)，用于标记，我是更新数据的源。于是，出现了 MOESI 协议

MOESI协议的状态机和演示示例我就不贴了（有兴趣可以上Berkeley上看看相关的课件），我们只需要理解MOESI协议允许 CPU Cache 间同步数据，于是也降低了对内存的操作，性能是非常大的提升，但是控制逻辑也非常复杂。

顺便说一下，与 MOESI 协议类似的一个协议是 MESIF，其中的 F 是 Forward，同样是把更新过的数据转发给别的 CPU Cache 但是，MOESI 中的 Owner 状态和MESIF 中的 Forward 状态有一个非常大的不一样—— Owner状态下的数据是dirty的，还没有写回内存，Forward状态下的数据是clean的，可以丢弃而不用另行通知。

需要说明的是，AMD用MOESI，Intel用MESIF。所以，F 状态主要是针对 CPU L3 Cache 设计的（前面我们说过，L3是所有CPU核心共享的）。（相关的比较可以参看StackOverlow上这个问题的答案）

程序性能

了解了我们上面的这些东西后，我们来看一下对于程序的影响。

示例一

首先，假设我们有一个64M长的数组，设想一下下面的两个循环：

const int LEN = 64*1024*1024;
int *arr = new int[LEN];

for (int i = 0; i < LEN; i += 2) arr[i] *= i;

for (int i = 0; i < LEN; i += 8) arr[i] *= i;

按我们的想法来看，第二个循环要比第一个循环少4倍的计算量，其应该也是要快4倍的。但实际跑下来并不是，在我的机器上，第一个循环需要127毫秒，第二个循环则需要121毫秒，相差无几。这里最主要的原因就是 Cache Line，因为CPU会以一个Cache Line 64Bytes最小时单位加载，也就是16个32bits的整型，所以，无论你步长是2还是8，都差不多。而后面的乘法其实是不耗CPU时间的。

示例二

我们再来看一个与缓存命中率有关的代码，我们以一定的步长increment 来访问一个连续的数组。

for (int i = 0; i < 10000000; i++) {
    for (int j = 0; j < size; j += increment) {
        memory[j] += j;
    }
}

我们测试一下，在下表中，表头是步长，也就是每次跳多少个整数，而纵向是这个数组可以跳几次（你可以理解为要几条Cache Line），于是表中的任何一项代表了这个数组有多少，而且步长是多少。比如：横轴是 512，纵轴是4，意思是，这个数组有 4*512 = 2048 个长度，访问时按512步长访问，也就是访问其中的这几项：[0, 512, 1024, 1536] 这四项。

表中同的项是，是循环1000万次的时间，单位是“微秒”（除以1000后是毫秒）

| count |   1    |   16  |  512  | 1024  |
------------------------------------------
|     1 |  17539 | 16726 | 15143 | 14477 |
|     2 |  15420 | 14648 | 13552 | 13343 |
|     3 |  14716 | 14463 | 15086 | 17509 |
|     4 |  18976 | 18829 | 18961 | 21645 |
|     5 |  23693 | 23436 | 74349 | 29796 |
|     6 |  23264 | 23707 | 27005 | 44103 |
|     7 |  28574 | 28979 | 33169 | 58759 |
|     8 |  33155 | 34405 | 39339 | 65182 |
|     9 |  37088 | 37788 | 49863 |156745 |
|    10 |  41543 | 42103 | 58533 |215278 |
|    11 |  47638 | 50329 | 66620 |335603 |
|    12 |  49759 | 51228 | 75087 |305075 |
|    13 |  53938 | 53924 | 77790 |366879 |
|    14 |  58422 | 59565 | 90501 |466368 |
|    15 |  62161 | 64129 | 90814 |525780 |
|    16 |  67061 | 66663 | 98734 |440558 |
|    17 |  71132 | 69753 |171203 |506631 |
|    18 |  74102 | 73130 |293947 |550920 |

我们可以看到，从 [9，1024] 以后，时间显著上升。包括 [17，512] 和 [18,512] 也显著上升。这是因为，我机器的 L1 Cache 是 32KB, 8 Way 的，前面说过，8 Way的有64组，每组8个Cache Line，当for-loop步长超过1024个整型，也就是正好 4096 Bytes时，也就是导致内存地址的变化是变化在高位的24bits上，而低位的12bits变化不大，尤其是中间6bits没有变化，导致全部命中同一组set，导致大量的cache 冲突，导致性能下降，时间上升。而 [16, 512]也是一样的，其中的几步开始导致L1 Cache开始冲突失效。

示例三

接下来，我们再来看个示例。下面是一个二维数组的两种遍历方式，一个逐行遍历，一个是逐列遍历，这两种方式在理论上来说，寻址和计算量都是一样的，执行时间应该也是一样的。

const int row = 1024;
const int col = 512
int matrix[row][col];

//逐行遍历
int sum_row=0;
for(int _r=0; _r<row; _r++) {
    for(int _c=0; _c<col; _c++){
        sum_row += matrix[_r][_c];
    }
}

//逐列遍历
int sum_col=0;
for(int _c=0; _c<col; _c++) {
    for(int _r=0; _r<row; _r++){
        sum_col += matrix[_r][_c];
    }
}

然而，并不是，在我的机器上，得到下面的结果。

逐行遍历：0.081ms
逐列遍历：1.069ms

执行时间有十几倍的差距。其中的原因，就是逐列遍历对于CPU Cache 的运作方式并不友好，所以，付出巨大的代价。

示例四

接下来，我们来看一下多核下的性能问题，参看如下的代码。两个线程在操作一个数组的两个不同的元素（无需加锁），线程循环1000万次，做加法操作。在下面的代码中，我高亮了一行，就是p2指针，要么是p[1]，或是 p[30]，理论上来说，无论访问哪两个数组元素，都应该是一样的执行时间。

void fn (int* data) {
    for(int i = 0; i < 10*1024*1024; ++i)
        *data += rand();
}

int p[32];

int *p1 = &p[0];
int *p2 = &p[1]; // int *p2 = &p[30];

thread t1(fn, p1);
thread t2(fn, p2);

然而，并不是，在我的机器上执行下来的结果是：

对于 p[0] 和 p[1] ：560ms
对于 p[0] 和 p[30]：104ms

这是因为 p[0] 和 p[1] 在同一条 Cache Line 上，而 p[0] 和 p[30] 则不可能在同一条Cache Line 上，CPU的缓存最小的更新单位是Cache Line，所以，这导致虽然两个线程在写不同的数据，但是因为这两个数据在同一条Cache Line上，就会导致缓存需要不断进在两个CPU的L1/L2中进行同步，从而导致了5倍的时间差异。

示例五

接下来，我们再来看一下另外一段代码：我们想统计一下一个数组中的奇数个数，但是这个数组太大了，我们希望可以用多线程来完成这个统计。下面的代码中，我们为每一个线程传入一个 id ，然后通过这个 id 来完成对应数组段的统计任务。这样可以加快整个处理速度。

int total_size = 16 * 1024 * 1024; //数组长度
int* test_data = new test_data[total_size]; //数组
int nthread = 6; //线程数（因为我的机器是6核的）
int result[nthread]; //收集结果的数组

void thread_func (int id) {
    result[id] = 0;
    int chunk_size = total_size / nthread + 1;
    int start = id * chunk_size;
    int end = min(start + chunk_size, total_size);

    for ( int i = start; i < end; ++i ) {
        if (test_data[i] % 2 != 0 ) ++result[id];
    }
}

然而，在执行过程中，你会发现，6个线程居然跑不过1个线程。因为根据上面的例子你知道 result[] 这个数组中的数据在一个Cache Line中，所以，所有的线程都会对这个 Cache Line 进行写操作，导致所有的线程都在不断地重新同步 result[] 所在的 Cache Line，所以，导致 6 个线程还跑不过一个线程的结果。这叫 False Sharing。

优化也很简单，使用一个线程内的变量。

void thread_func (int id) {
    result[id] = 0;
    int chunk_size = total_size / nthread + 1;
    int start = id * chunk_size;
    int end = min(start + chunk_size, total_size);

    int c = 0; //使用临时变量，没有cache line的同步了
    for ( int i = start; i < end; ++i ) {
        if (test_data[i] % 2 != 0 ) ++c;
    }
    result[id] = c;
}

我们把两个程序分别在 1 到 32 个线程上跑一下，得出的结果画一张图如下所示（横轴是线程数，纵轴是完成统的时间，单位是微秒）：

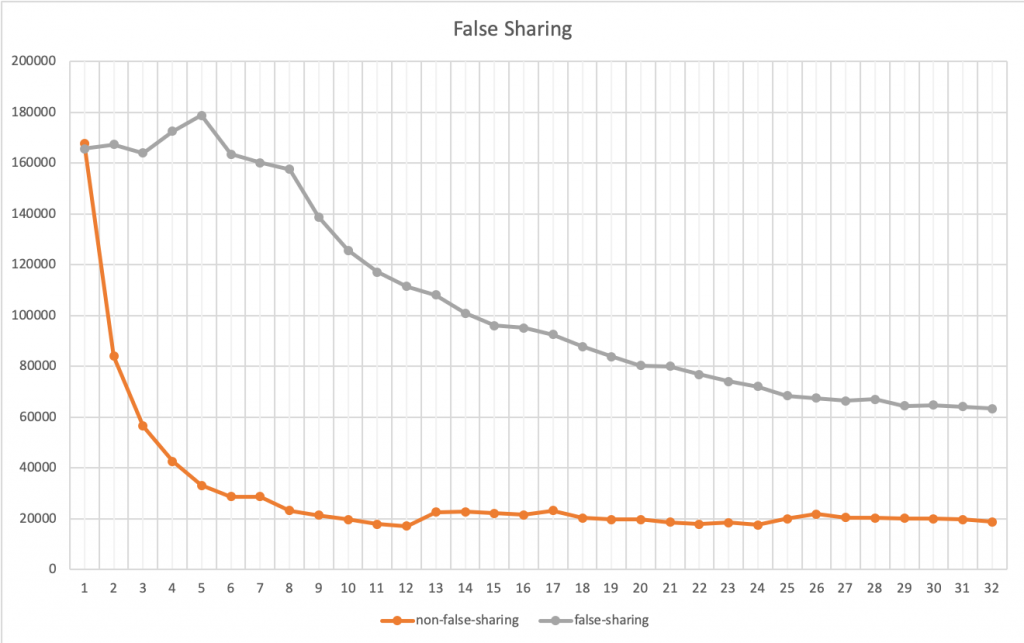
上图中，我们可以看到，灰色的曲线就是第一种方法，橙色的就是第二种（用局部变量的）方法。当只有一个线程的时候，两个方法相当，基本没有什么差别，但是在线程数增加的时候的时候，你会发现，第二种方法的性能提高的非常快。直到到达6个线程的时候，开始变得稳定（前面说过，我的CPU是6核的）。而第一种方法无论加多少线程也没有办法超过第二种方法。因为第一种方法不是CPU Cache 友好的。也就是说，第二种方法，只要我的CPU核数足够多，就可以做到线性的性能扩展，让每一个CPU核都跑起来，而第一种则不能。

篇幅问题，示例就写到这里，相关的代码参看我的Github相关仓库。